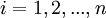Многопродуктовая статическая модель с ограниченной вместимостью склада
Материал из Supply Chain Management Encyclopedia
WikiSysop (обсуждение | вклад) (Содержимое страницы заменено на «<math>\, D_{i}</math> - интенсивность спроса на ресурс;») |
WikiSysop (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| - | <math>\, D_{i}</math> - интенсивность спроса на ресурс; | + | Рассматривается случай статического объема спроса. |
| + | |||
| + | ==Основные предположения модели== | ||
| + | |||
| + | * рассматривается задача управления несколькими видами запаса; | ||
| + | |||
| + | * складское пространство ограничено; | ||
| + | |||
| + | * интенсивность спроса на ресурс (количество единиц ресурса, потребляемых в единицу времени) - постоянная величина (константа); | ||
| + | |||
| + | * закупочная цена единицы ресурса постоянна (константа, не зависит от объема заказа); | ||
| + | |||
| + | * удельные затраты на хранение в единицу времени (затраты на хранение единицы ресурса в единицу времени) - постоянная величина (константа); | ||
| + | |||
| + | * затраты на оформление, связанные с размещением заказа, - постоянная величина (константа); | ||
| + | |||
| + | * заказ размещается и пополняется мгновенно; | ||
| + | |||
| + | * дефицит отсутствует. | ||
| + | |||
| + | ==Основные обозначения== | ||
| + | |||
| + | Для запасов вида <math>\, i</math>, <math>\, i=1,2,...,n</math>: | ||
| + | |||
| + | * <math>\, D_{i}</math> - интенсивность спроса на ресурс; | ||
| + | |||
| + | * <math>\, h_{i}</math> - удельные затраты на хранение; | ||
| + | |||
| + | * <math>\, K_{i}</math> - затраты на оформление, связанные с размещением заказа; | ||
| + | |||
| + | * <math>\, TCU(y)</math> - суммарные затраты в единицу времени; | ||
| + | |||
| + | * <math>\, y_{i}</math> - объем заказа (количество единиц ресурса); | ||
| + | |||
| + | * <math>\, y_{i}^{*}</math> - экономичный (оптимальный в смысле минимизации суммарных затрат в единицу времени) размер заказа; | ||
| + | |||
| + | * <math>\, a_{i}</math> - необходимое пространство для хранения единицы товара; | ||
| + | |||
| + | * <math>\, A</math> - максимальное складское пространство для хранения товаров <math>\, n</math> видов. | ||
| + | |||
| + | ==Оптимальная стратегия управления запасами== | ||
| + | |||
| + | В соответствии с предположениями модели динамику изменения запаса ресурса <math>\, i</math> имеет вид, рис. 1: | ||
| + | |||
| + | [[File:Z3pic1.png]] | ||
| + | |||
| + | '''Рис. 1.''' Динамика изменения запаса ресурса <math>\, i</math>. | ||
| + | |||
| + | Многопродуктовая статическая модель с ограниченной вместимостью склада может быть формализована как задача нелинейного программирования: | ||
| + | |||
| + | <math>\min TCU(y_{1} ,y_{2} ,...,y_{n} )=\sum \limits _{i=1}^{n}\left(\frac{K_{i} D_{i} }{y_{i} } +\frac{h_{i} y_{i} }{2} \right)</math> | ||
| + | |||
| + | <math>\sum \limits _{i=1}^{n}a_{i} y_{i} \le A</math> | ||
| + | |||
| + | <math>\, y_{i} >0</math> | ||
| + | |||
| + | <math>\,i=1,2,...,n</math>. | ||
| + | |||
| + | |||
| + | ''' Оптимальная стратегия управления запасами''' | ||
| + | |||
| + | Для сформулированной выше задачи нелинейного программирования функция Лагранжа имеет вид: | ||
| + | |||
| + | <math>L(\lambda ,y_{1} ,y_{2} ,...,y_{n} )=TCU(y_{1} ,y_{2} ,...,y_{n} )-\lambda \left(\sum \limits _{i=1}^{n}a_{i} y_{i} -A\right)=</math> | ||
| + | |||
| + | <math> =\sum \limits _{i=1}^{n}\left(\frac{K_{i} D_{i} }{y_{i} } +\frac{h_{i} y_{i} }{2} \right) -\lambda \left(\sum \limits _{i=1}^{n}a_{i} y_{i} -A\right)</math> , | ||
| + | |||
| + | здесь <math>\, \lambda <0</math> - множитель Лагранжа. | ||
| + | |||
| + | Функция Лагранжа для многопродуктовой статической модели с ограниченной вместимостью склада является выпуклой, следовательно, оптимальное значение <math>\, \lambda</math> и <math>\, y_{i}</math> могут быть найдены из условий первого порядка: | ||
| + | |||
| + | <math> \frac{\partial L}{\partial \lambda } =-\sum \limits _{i=1}^{n}a_{i} y_{i} +A=0</math> (ограничение по вместимости склада в оптимальной точке); | ||
| + | |||
| + | <math>\frac{\partial L}{\partial y_{i} } =-\frac{K_{i} D_{i} }{y_{i}^{2} } +\frac{h_{i} }{2} -\lambda a_{i} =0</math> . | ||
| + | |||
| + | Решение второго уравнения имеет вид: | ||
| + | |||
| + | <math>y_{i}^{*} =\sqrt{\frac{2K_{i} D_{i} }{h_{i} -2\lambda ^{*} a_{i} } }</math> . | ||
| + | |||
| + | Значение, приближенное к оптимальному решению значению <math>\, \lambda ^{*}</math> с наперед заданной точностью можно найти следующим образом: | ||
| + | |||
| + | 1. Задать начальное значение <math>\, \lambda =0</math> | ||
| + | |||
| + | 2. Задать величину <math>\, \varepsilon</math> уменьшения значения <math>\, \lambda</math> (точность) | ||
| + | |||
| + | 3. Последовательно уменьшать <math>\, \lambda</math> на величину <math>\, \varepsilon</math>, подставляя значение <math>\, \lambda</math> в <math>y_{i} =\sqrt{\frac{2K_{i} D_{i} }{h_{i} -2\lambda a_{i} } }</math> и проверяя выполнение ограничения по вместимости склада. | ||
| + | |||
| + | Оптимальная стратегия управления запасами в рассматриваемой модели имеет вид: | ||
| + | |||
| + | '''Шаг 1.''' Вычислить оптимальные объемы заказов каждого вида, не учитывая ограничение на вместимость склада (см. раздел [[Экономичный размер заказа]]) по формуле: | ||
| + | |||
| + | <math>y_{i}^{**} =\sqrt{\frac{2K_{i} D_{i} }{h_{i} } }</math>, | ||
| + | |||
| + | <math>\, i=1,2,...,n</math>. | ||
| + | |||
| + | '''Шаг 2.''' При найденных значениях <math>\, y_{i}^{**}</math>, <math>\, i=1,2,...,n</math> проверить выполнение ограничения по вместимости склада. Если это ограничение выполняется, то набор величин <math>\, y_{i}^{*}</math>, <math>\, i=1,2,...,n</math> является оптимальным решением для многопродуктовой статической модели с ограниченной вместимостью склада. В противном случае, оптимальным решением является набор <math>\, y_{i}^{*}</math>, <math>\, i=1,2,...,n</math> | ||
Версия 11:21, 4 июня 2011
Рассматривается случай статического объема спроса.
Основные предположения модели
- рассматривается задача управления несколькими видами запаса;
- складское пространство ограничено;
- интенсивность спроса на ресурс (количество единиц ресурса, потребляемых в единицу времени) - постоянная величина (константа);
- закупочная цена единицы ресурса постоянна (константа, не зависит от объема заказа);
- удельные затраты на хранение в единицу времени (затраты на хранение единицы ресурса в единицу времени) - постоянная величина (константа);
- затраты на оформление, связанные с размещением заказа, - постоянная величина (константа);
- заказ размещается и пополняется мгновенно;
- дефицит отсутствует.
Основные обозначения
Для запасов вида  ,
, 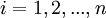 :
:
-
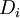 - интенсивность спроса на ресурс;
- интенсивность спроса на ресурс;
-
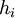 - удельные затраты на хранение;
- удельные затраты на хранение;
-
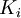 - затраты на оформление, связанные с размещением заказа;
- затраты на оформление, связанные с размещением заказа;
-
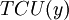 - суммарные затраты в единицу времени;
- суммарные затраты в единицу времени;
-
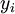 - объем заказа (количество единиц ресурса);
- объем заказа (количество единиц ресурса);
-
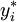 - экономичный (оптимальный в смысле минимизации суммарных затрат в единицу времени) размер заказа;
- экономичный (оптимальный в смысле минимизации суммарных затрат в единицу времени) размер заказа;
-
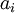 - необходимое пространство для хранения единицы товара;
- необходимое пространство для хранения единицы товара;
-
 - максимальное складское пространство для хранения товаров
- максимальное складское пространство для хранения товаров  видов.
видов.
Оптимальная стратегия управления запасами
В соответствии с предположениями модели динамику изменения запаса ресурса  имеет вид, рис. 1:
имеет вид, рис. 1:
Рис. 1. Динамика изменения запаса ресурса  .
.
Многопродуктовая статическая модель с ограниченной вместимостью склада может быть формализована как задача нелинейного программирования:
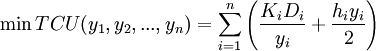
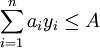
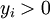
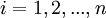 .
.
Оптимальная стратегия управления запасами
Для сформулированной выше задачи нелинейного программирования функция Лагранжа имеет вид:
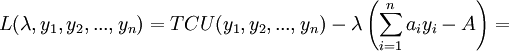
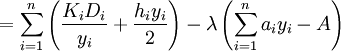 ,
,
здесь 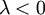 - множитель Лагранжа.
- множитель Лагранжа.
Функция Лагранжа для многопродуктовой статической модели с ограниченной вместимостью склада является выпуклой, следовательно, оптимальное значение 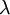 и
и 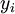 могут быть найдены из условий первого порядка:
могут быть найдены из условий первого порядка:
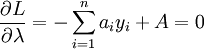 (ограничение по вместимости склада в оптимальной точке);
(ограничение по вместимости склада в оптимальной точке);
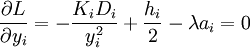 .
.
Решение второго уравнения имеет вид:
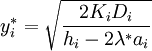 .
.
Значение, приближенное к оптимальному решению значению 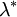 с наперед заданной точностью можно найти следующим образом:
с наперед заданной точностью можно найти следующим образом:
1. Задать начальное значение 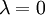
2. Задать величину 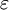 уменьшения значения
уменьшения значения 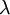 (точность)
(точность)
3. Последовательно уменьшать 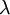 на величину
на величину 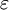 , подставляя значение
, подставляя значение 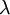 в
в 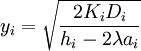 и проверяя выполнение ограничения по вместимости склада.
и проверяя выполнение ограничения по вместимости склада.
Оптимальная стратегия управления запасами в рассматриваемой модели имеет вид:
Шаг 1. Вычислить оптимальные объемы заказов каждого вида, не учитывая ограничение на вместимость склада (см. раздел Экономичный размер заказа) по формуле:
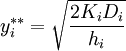 ,
,
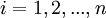 .
.
Шаг 2. При найденных значениях 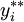 ,
, 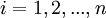 проверить выполнение ограничения по вместимости склада. Если это ограничение выполняется, то набор величин
проверить выполнение ограничения по вместимости склада. Если это ограничение выполняется, то набор величин 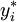 ,
, 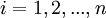 является оптимальным решением для многопродуктовой статической модели с ограниченной вместимостью склада. В противном случае, оптимальным решением является набор
является оптимальным решением для многопродуктовой статической модели с ограниченной вместимостью склада. В противном случае, оптимальным решением является набор 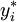 ,
,