Сетевые модели
Материал из Supply Chain Management Encyclopedia
Известно, что одной из основных характеристик эффективности алгоритма является скорость его работы. Несмотря на вычислительные возможности современной компьютерной техники, решение многих оптимизационных задач, даже малой размерности, занимает необозримое количество времени. Вместе с тем, если удается сформулировать задачу в виде сетевой модели, то шансы получить решение значительно увеличиваются, поскольку для решения таких задач используются специальные алгоритмы. По мнению специалистов в области исследования операций, не менее 70\% задач математического программирования имеют сетевую интерпретацию. В этом разделе рассмотрены транспортные модели и задача коммивояжера.
Основные определения
Пусть  - некоторое конечное множество, будем называть его множеством узлов. Правило
- некоторое конечное множество, будем называть его множеством узлов. Правило 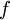 , ставящее в соответствие каждому элементу
, ставящее в соответствие каждому элементу  элемент
элемент  , называется однозначным отображением
, называется однозначным отображением 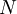 в
в 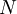 . Многозначное отображение
. Многозначное отображение  множества
множества 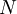 в
в 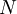 - это правило, которое каждому элементу
- это правило, которое каждому элементу  ставит в соответствие некоторое подмножество
ставит в соответствие некоторое подмножество  (при этом допускается
(при этом допускается 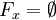 ). Пара
). Пара 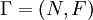 называется графом, если
называется графом, если 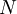 - некоторое конечное множество, a
- некоторое конечное множество, a  - отображение
- отображение 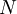 в
в 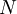 . В качестве примера, можем рассмотреть цепь поставок, в которой поставщики, производитель и потребители всех уровней являются узлами графа, а отображение
. В качестве примера, можем рассмотреть цепь поставок, в которой поставщики, производитель и потребители всех уровней являются узлами графа, а отображение  - это все возможные маршруты движения материалов (товаров).
- это все возможные маршруты движения материалов (товаров).
В дальнейшем элементы множества 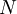 будем изображать точками на плоскости, а пары точек
будем изображать точками на плоскости, а пары точек 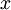 и
и 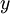 , для которых
, для которых 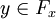 , соединять непрерывной линией со стрелкой, направленной от
, соединять непрерывной линией со стрелкой, направленной от 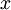 к
к 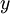 . Тогда каждый элемент множества
. Тогда каждый элемент множества 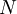 называется вершиной или узлом графа, а пара элементов
называется вершиной или узлом графа, а пара элементов 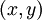 , в которой
, в которой 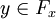 - дугой графа. Множество дуг в графе будем обозначать
- дугой графа. Множество дуг в графе будем обозначать 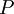 . Задание множества дуг в графе
. Задание множества дуг в графе 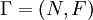 определяет отображение
определяет отображение  и, наоборот, отображение
и, наоборот, отображение  определяет множество
определяет множество 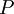 . Поэтому граф можно записывать как в виде
. Поэтому граф можно записывать как в виде 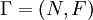 , так и в виде
, так и в виде  .
.
Ребром графа  называется множество из двух элементов
называется множество из двух элементов 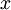 ,
, 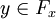 , для которых или
, для которых или  , или
, или  . В отличие от дуги для ребра ориентация роли не играет. Ребра будем обозначать буквами
. В отличие от дуги для ребра ориентация роли не играет. Ребра будем обозначать буквами  ,
,  , а множество ребер -
, а множество ребер - 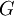 .
.
Под цепью будем понимать последовательность ребер 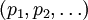 , в которой у каждого ребра
, в которой у каждого ребра 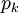 одна из граничных вершин является также граничной для
одна из граничных вершин является также граничной для 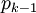 , другая - граничной для
, другая - граничной для 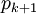 .
.
Цикл - это конечная цепь, начинающаяся в некоторой вершине и оканчивающаяся в той же вершине. Граф называется связным, если любые две его вершины можно соединить цепью.
Сеть - это граф, множество ребер которого задано некоторой числовой функцией.
С каждой сетью связан определенный поток (например, поток газа в газопроводах, поток информации в компьютерных сетях). Будем считать, что потоки в сети ограничены пропускной способностью ее ребер, которая может быть как конечной, так и бесконечной.
2. Транспортная задача
В данном разделе рассматривается специальный класс задач линейного программирования - транспортные модели. Свое название они получили благодаря классической задаче о перевозке некоторого товара из нескольких пунктов отправления (производство, склады) в несколько пунктов назначения (потребители, магазины). Другими словами имеется два типа узлов:
1) истоки (пункты отправления)
2) стоки (пункты назначения)
В транспортной модели предполагается, что объемы предложения и спроса известны, стоимость перевозки по какому-либо маршруту прямо пропорциональна объему перевозимого груза. Задача состоит в построении такого плана перевозок, при котором суммарные транспортные затраты минимальны при условии. При этом вывозится вся продукция из пунктов отправления и удовлетворяется весь спрос в пунктах назначения.
Необходимо заметить, что с одной стороны математический аппарат транспортных моделей, применим к целому ряду реальных задач, в которых ничего никуда не перевозится (задача об оптимальном назначении работников, планирование производства по месяцам и т.д.). С другой стороны, далеко не все задачи логистики входят в класс транспортных задач линейного программирования (задача коммивояжера, задача о кратчайшем пути).
2.1 Способы задания транспортной задачи
В настоящем разделе будут использоваться три способа задания транспортной задачи: аналитический, сетевой и табличный.
- Аналитический способ
Рассмотрим транспортную задачу в классической постановке. Пусть имеется  пунктов производства и
пунктов производства и  пунктов потребления. Зададим таблицу транспортных издержек, состоящую из элементов
пунктов потребления. Зададим таблицу транспортных издержек, состоящую из элементов  - стоимости перевозки единицы продукции от
- стоимости перевозки единицы продукции от  -го производителя к
-го производителя к  -му потребителю:
-му потребителю:
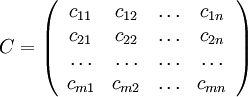
При постановке задачи все элементы транспортной таблицы  известны.
известны.
Рассмотрим таблицу перевозок, состоящую из переменных  - количества перевозимой продукции от
- количества перевозимой продукции от  -го производителя к
-го производителя к  -му потребителю:
-му потребителю:

При постановке задачи элементы таблицы перевозок 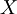 неизвестны - это переменные, значения которых необходимо определить.
неизвестны - это переменные, значения которых необходимо определить.
Объемы производства и потребления обозначим соответственно  и
и  .
.
- Сетевой способ
На рисунке показано общее представление транспортной задачи в виде сети с двумя типами узлов, соответствующих  пунктам отправления и
пунктам отправления и  пунктам назначения. Дуги, соединяющие узлы сети, соответствуют маршрутам между пунктами отправления и назначения. Каждой дуге
пунктам назначения. Дуги, соединяющие узлы сети, соответствуют маршрутам между пунктами отправления и назначения. Каждой дуге  соответствуют затраты
соответствуют затраты  и количество перевозимого груза
и количество перевозимого груза  :
:
- Табличный способ
Строки таблицы 2 соответствуют пунктам отправления, а столбцы - пунктам назначения. В ячейках  указываем параметры
указываем параметры  и переменные
и переменные  , объемы потребления установлены в ячейках строки
, объемы потребления установлены в ячейках строки  , объемы производства - в столбце
, объемы производства - в столбце 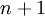 :
:
Таблица 2
2.2 Математическая модель транспортной задачи
Целью оптимизации в транспортной задаче является минимизация затрат на перевозку. Удельные затраты приведены в транспортной таблице $C$ , переменные образуют таблицу перевозок $X$ . Для составления целевой функции необходимо поэлементно перемножить таблицы $C$ и $X$ и сложить полученные произведения. Тем самым получим суммарные издержки:

Выписать систему ограничений не представляет большого труда, если составлена сеть транспортной задачи. Рассмотрим пункта отправления под номером $i$ . Объем вывозимого груза в пункты назначения должен равняться имеющимся здесь запасам:
$\sum \limits _{j=1}^{n}x_{ij} =a_{i} $ , где $i=1,2,\ldots m$
Аналогично с пунктом назначения под номером $j$ : объем доставленного сюда груза из пунктов отправления должен равняться спросу пункта $j$ :
$\sum \limits _{i=1}^{m}x_{ij} =b_{j} $ , где $j=1,2,\cdots n$
Укажем, также неотрицательность и целочисленность переменных:
$x_{ij} \ge 0$ , $x_{ij} $ - целые.
{\it 2.}{\it 3}{\it Пример}
Фирма по производству мебели "Комфорт" имеет два склада. В начале недели поступили заказы от трех потребителей на 6, 7 и 11 шкафов. На первом складе имеется 15, на втором складе - 9 шкафов. Пополнение запасов до конца недели не предвидится. Стоимость перевозки одного шкафа с первого склада потребителям 1, 2, 3 равна соответственно 600, 100, 400 руб. Со второго склада{\it }- 1200, 200, 800 руб. соответственно.
Необходимо составить план перевозок, минимизирующий общую сумму транспортных расходов.
Решение задачи начнем с построения сети:
Задача сбалансирована, поскольку суммарные запасы на складах 15+9=24 совпадает с объемом спроса: 6+7+11=24. Математическая постановка имеет следующий вид:
$$\min z=\min (600x_{11} +100x_{12} +400x_{13} +1200x_{21} +200x_{22} +800x_{23} )$$
$$\left\{\begin{array}{l} {x_{11} +x_{12} +x_{13} =15} \\ {x_{21} +x_{22} +x_{23} =9} \\ {x_{11} +x_{21} =6} \\ {x_{12} +x_{22} =7} \\ {x_{13} +x_{23} =11} \\ {x_{ij} \ge 0,\, \, x_{ij} -\, F5;.,\, \, i=1,2;\, j=1,2,3} \end{array}\right. $$
{\it 2.4 Условие сбалансированности транспортной модели.}
- {\bf Условие баланса}
Говорят, что транспортная задача сбалансирована, если выполнено условие баланса - суммарный объем производства равен суммарному объему потребления:
$$\sum \limits _{i=1}^{m}a_{i} =\sum \limits _{j=1}^{n}b_{j} $$
В этом случае задача имеет оптимальное решение. Условие баланса не выполняется в двух случаях: перепроизводстве и дефиците.
- {\bf Перепроизводство}
При перепроизводстве имеем неравенство:
$$\sum \limits _{i=1}^{m}a_{i} >\sum \limits _{j=1}^{n}b_{j} $$
Решение задачи транспортного типа при условии перепроизводства зависит от наличия штрафов за неполный вывоз товаров со склада:
1) штрафы отсутствуют. Следовательно, целевая функция (суммарные затраты) не меняется, часть товаров просто остается на складах. Отразим это в математической постановке, заменив знак равенства в ограничениях на объемы производства на неравенство:
$$\min z=\min (c_{11} x_{11} +c_{12} x_{12} +\ldots +c_{mn} x_{mn} )=\min \sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}c_{ij} x_{ij} $$
$\sum \limits _{j=1}^{n}x_{ij} \le a_{i} $ , где $i=1,2,\ldots m$
$\sum \limits _{i=1}^{m}x_{ij} =b_{j} $ , где $j=1,2,\cdots n$
$x_{ij} \ge 0$ , $x_{ij} $ - целые.
2) существуют штрафы за хранение оставшегося товара по крайней мере в одном пункте отправления. Размер штрафа пропорционален количеству единиц товара. В этом случае в целевой функции необходимо учесть появившиеся издержки. Сбалансируем задачу с помощью добавления фиктивного потребителя. Будем предполагать, что этот потребитель обладает спросом в объеме $b_{n+1} =\sum \limits _{i=1}^{m}a_{i} -\sum \limits _{j=1}^{n}b_{j} $ . Штраф за оставшуюся в пункте отправления под номером $i$ единицу товара обозначим $c_{in+1} $ . Таким образом, в транспортной таблице и таблице перевозок появляется дополнительный столбец с номером $n+1$ . В итоге имеем новую задачу, для которой выполнено условие баланса.
Пример.
В следующей задаче перепроизводство составляет 4 единицы:
Штраф за остаток единицы товара на первом складе отсутствует, на втором - равен 2, на третьем -1. Введем фиктивного потребителя с объемом спроса 4:
- {\bf Дефицит}
При дефиците имеем неравенство:
$$\sum \limits _{i=1}^{m}a_{i} <\sum \limits _{j=1}^{n}b_{j} $$
Решение задачи транспортного типа при условии дефицита зависит от наличия штрафов за неудовлетворенный спрос:
1) штрафы отсутствуют. Следовательно, целевая функция (суммарные затраты) не меняется, часть товара клиентам просто не доставляется. Отразим это в математической постановке, заменив знак равенства в ограничениях на объемы спроса на неравенство:
$$\min z=\min (c_{11} x_{11} +c_{12} x_{12} +\ldots +c_{mn} x_{mn} )=\min \sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}c_{ij} x_{ij} $$
$\sum \limits _{j=1}^{n}x_{ij} =a_{i} $ , где $i=1,2,\ldots m$
$\sum \limits _{i=1}^{m}x_{ij} \le b_{j} $ , где $j=1,2,\cdots n$
$x_{ij} \ge 0$ , $x_{ij} $ - целые.
2) существуют штрафы за неудовлетворенный спрос, по крайней мере, одного потребителя. Размер штрафа пропорционален количеству единиц не доставленного товара. В этом случае в целевой функции необходимо учесть появившиеся издержки. Сбалансируем задачу с помощью добавления фиктивного производителя. Будем предполагать, что этот производитель обладает запасами в недостающем объеме $a_{m+1} =\sum \limits _{j=1}^{n}b_{j} -\sum \limits _{i=1}^{m}a_{i} $ . Штраф за каждую единицу товара, которая не была доставлена потребителю под номером $j$ , обозначим $c_{m+1j} $ . Таким образом, в транспортной таблице и таблице перевозок появляется дополнительная строка с номером $m+1$ . В итоге имеем новую задачу, для которой выполнено условие баланса.
Пример.
В следующей задаче дефицит равен 7 единицам:
Штраф за неудовлетворенный спрос первого и четвертого потребителя отсутствует. Для второго потребителя штраф равен 3 , для третьего потребителя - 1. Введем фиктивного производителя с запасом в 7 единиц:
{\it 2.}{\it 5}{\it Определение начального решения}
В отличие от задач линейного программирования, рассмотренных в Теме 1, для корректного решения задач транспортного типа с помощью надстройки MS Excel "Поиск решения" необходимо указывать начальное решение, которое является допустимым. В настоящем пункте приводятся два метода поиска допустимого решения для задач транспортного типа: метод {\it северо-западного элемента} и метод {\it минимального элемента}.
- {\bf Метод северо-западного элемента}
Алгоритм:
1) Переменной в верхней левой ячейки таблицы присваивается максимальное значение, допускаемое ограничениями на спрос и предложение
2) Вычеркивается строка (или столбец) с полностью реализованным предложением (или спросом). Корректируется объем спроса в соответствующем столбце (или предложение в строке).
3) Если осталась таблица, состоящая только из одной строки или только одного столбца, ее ячейки заполняются согласно имеющемуся предложению и спросу. В противном случае переходим к первому этапу.
Определим начальное решение методом северо-западного элемента в транспортной задаче фирмы "Комфорт" (стрелками указана последовательность определения значения переменных):
- {\bf Метод }{\bf минимального}{\bf элемента}
Алгоритм:
1) В транспортной таблице определяется ячейка с минимальными затратами. Переменной в этой ячейке присваивается максимальное значение, допускаемое ограничениями на спрос и предложение
2) Вычеркивается строка (или столбец) с полностью реализованным предложением (или спросом). Корректируется объем спроса в соответствующем столбце (или предложение в строке).
3) Если осталась таблица, состоящая только из одной строки или только одного столбца, ее ячейки заполняются согласно имеющемуся предложению и спросу. В противном случае переходим к первому этапу.
Определим начальное решение методом минимального элемента в транспортной задаче фирмы "Комфорт" (стрелками указана последовательность определения значения переменных):
{\it 2.}{\it 6}{\it Решение транспортной задачи средствами MS E}{\it x}{\it cel}{\it (см. файл }{\it }2К{\it омфорт}{\it Транспортная задача}{\it .xls})
Откроем лист "допустимое решение". Определим оптимальный план перевозок, согласно поступившим заказам для фирмы "Комфорт" из примера пункта 2.3.
Как и при решении задачи темы 1, ячейки, содержащие {\it параметры} задачи, будем выделять серым цветом и обводить в синие рамки. Ячейки, содержащие {\it переменные}, будем обводить красными рамками.
{\bf Исходные данные}
В ячейках С6:Е7 указываем стоимость перевозки с каждого склада каждому потребителю
В ячейках С12:Е13 - указываем начальные значения объемов перевозок, определенные по методу минимального элемента.
В ячейках Н12:Н13 указываем имеющиеся на складах запасы продукции
В ячейках С16:Е16 устанавливаем значения объемов заказа клиентов 1, 2 и 3
{\bf Ограничения}
В ячейке F12 посчитаем суммарное количество товаров, вывозимое с первого склада с помощью формулы:
=СУММ(C12:E12).
В ячейке F13 указываем суммарное количество товаров, вывозимое со второго склада.
Аналогично определяем количество шкафов, доставляемое каждому клиенту. В ячейке С14 посчитаем суммарное количество товаров, доставленных первому клиенту помощью формулы:
=СУММ(C12:C13).
Для определения количества продукции, полученной вторым и третьим клиентами, скопируем эту формулу в ячейки D14:E14. Обратим внимание, что в данном случае используется относительная адресация, то есть при копировании аргументы функции автоматически корректируются соответственно столбцам D и E.
{\bf Целевая функция}
В ячейке С20 подсчитывается суммарная стоимость перевозок с помощью формулы:
=СУММПРОИЗВ(C6:E7;C12:E13).
Другими словами, здесь поэлементно перемножаются транспортная таблица и таблица перевозок, полученные произведения складываются.
{\bf Поиск решения}
Перейдем на лист "оптимальное решение" и откроем надстройку "Поиск решения".
{\it Установить целевую ячейку.} Указываем ячейку С20 - суммарная стоимость
{\it Изменяемые ячейки.} Выбираем массив \$C\$12:\$E\$13 в качестве изменяемых ячеек.
{\it Ограничения.} Добавляем ограничения на имеющиеся запасы: \$F\$12:\$F\$13= \$H\$12:\$H\$13, на спрос: \$C\$14:\$E\$14= \$C\$16:\$E\$16, а также целочисленность и неотрицательность переменных: \$C\$12:\$E\$13=целое, \$C\$12:\$E\$13?0.
Нажимаем кнопку Параметры и устанавливаем флаг в поле Линейная модель. Возвращаемся в диалоговое окно Поиска решения и нажимаем Выполнить.
Суммарная стоимость перевозок равна 10200 руб. Этот результат был неожиданностью для отдела доставки фирмы "Комфорт". Напомним, что при начальном решении, определенного методом минимального элемента, вывоз товара осуществлялся сначала по самому дешевому маршруту, потом по следующему по стоимости и так далее. Разумеется, в первую очередь предполагалось вывезти максимально возможное количество шкафов с первого склада второму клиенту - ведь стоимость доставки здесь всего 100 руб. Но при этом суммарные транспортные издержки существенно отличались от полученного оптимального значения и составляли 13500 руб. Кроме того, в оптимальном плане перевозок с первого склада второму потребителю не везется ничего! Как же объяснить, что "Поиск решения" "проигнорировал" в оптимальном решении самые низкие затраты? Легко заметить, что в решении, полученном по методу минимального элемента, товар перевозится как по самому дешевому маршруту (с первого склада второму клиенту), так и по самому дорогому (со второго склада первому клиенту). При этом стоимость перевозки одного шкафа по последнему маршруту составляет 1200 руб., и в решении предлагается перевозить по этой цене 6 шкафов. Теперь рассмотрим оптимальный план перевозок. Да, по самому дешевому маршруту мы ничего не везем, но мы также ничего не перевозим и по самому дорогому маршруту.
{\bf 3 Распределительная задача}
Как уже отмечалось, в сетевом способе задания таких задач существует два типа узлов: истоки и стоки. Распределительная задача - это наиболее общая постановка сетевой задачи. Она отличается от транспортной модели наличием узлов в сети трех типов:
1){\it Истоки}
2) {\it Стоки}
3) {\it Промежуточные}{\it }{\it узлы}
Как и в транспортных моделях, каждый исток характеризуется предложением, сток - спросом. Промежуточные узлы имеют нулевой спрос и предложение. Следовательно, распределительная задача включает в себя, как частный случай, транспортную модель.
{\it 3.1 Математическая постановка распределительной задачи}
Введем следующие обозначения:
{\it N}{\it - }множество узлов в сети;
$\displaystyle n$ - число узлов в сети,
$\displaystyle G$ - множество всех ребер (дуг) в сети,
$x_{ij} $ - величина потока, проходящего по дуге $(i,j)$ ,
$c_{ij} $ - затраты на единицу потока из $i$ в $j$ ,
$l_{ij} $ - нижняя граница потока из $i$ в $j$ ,
$u_{ij} $ - верхняя граница потока из $i$ в $j$ ,
$b_{j} $ - производительность (спрос или предложение) в узле $j$ ,
$\displaystyle \left(i,j\right)$ - ребро (дуга) сети.
Будем понимать объем спроса в стоках как производительность со знаком минус. Это позволяет записать условие баланса модели в виде:
$$\sum \limits _{j\in N}b_{j} =0$$
{\bf Целевая функция}
Рассмотрим задачу нахождения потока в сети минимальной стоимости, следовательно, целевая функция примет вид:
$$\min \sum \limits _{(i,j)\in G}c_{ij} x_{ij} $$
(сравните с целевой функцией транспортной задачи).
{\bf Ограничения}
1) {\it Ограничения}{\it , накладываемые пропускной способностью ребер}
Каждая переменная $x_{ij} $ определяет поток, протекающий по ребру $(i,j)$ , следовательно, она должна удовлетворять ограничениям на пропускную способность этого ребра:
$$l_{ij} \le x_{ij} \le u_{ij} ,\; (i,j)\in G,$$
Для каждого узла должно быть выполнено основное соотношение для потока
2) {\it Основное соотношение для потока}
Для {\it }каждого узла сети должно выполняться соотношение:
Вытекающий поток - Втекающий поток = Производительность узла
Или в принятых обозначениях:
$\sum \limits _{(j,i)\in G}x_{ji} -\sum \limits _{(i,j)\in G}x_{ij} =b_{j} $ , $j$ =1,2,... $n$
Кроме того, должны выполняться условия на неотрицательность и целочисленность потока:
$$x_{ij} \ge 0$$
$\displaystyle x_{ij} $ - целые.
Окончательно, математическая модель распределительной задачи принимает вид:
$$\min \sum \limits _{(i,j)\in G}c_{ij} x_{ij} $$
$$l_{ij} \le x_{ij} \le u_{ij} ,\; (i,j)\in G,$$
$$\sum \limits _{j\in N}b_{j} =0,$$
$\sum \limits _{(j,i)\in G}x_{ji} -\sum \limits _{(i,j)\in G}x_{ij} =b_{j} $ , $j$ =1,2,... $n$
$$x_{ij} \ge 0$$
$\displaystyle x_{ij} $ - целые
{\it 3.1. Задача о кратчайшем пути}
Данная задача состоит в определении кратчайшего пути между двумя узлами транспортной сети. Такими моделями могут формализоваться многие реальные задачи, например, прокладка маршрута, график замены оборудования, задача о загрузке.
{\bf Пример.} Фирма по производству мебели "Комфорт" получила от иногороднего клиента заказ на изготовление и доставку эксклюзивного стола. В отделе логистики фирмы имеется схема дорог с нанесенными на ней расстояниями между населенными пунктами:
В городе 1 расположено производство фирмы "Комфорт", а пункт назначения - в городе 7. Стол был изготовлен в срок, оставалось определить самый маршрут доставки минимальной продолжительности.
Решение.
Начнем с проверки баланса модели. Фирма получила заказ на один стол. Напомним, что спрос понимаем как отрицательную производительность, следовательно, условие баланса выполнено:
$$1+(-1)=0$$
Пусть $x_{ij} $ - величина потока из города $i$ в город $j$ . Под затратами будем понимать расстояние между городами, тогда целевая функция принимает вид:
$$\min z=\min (10x_{12} +40x_{13} +30x_{14} +55x_{25} +15x_{24} +12x_{34} +18x_{36} +$$
$$+40x_{45} +60x_{47} +33x_{46} +15x_{57} +20x_{67} )$$
Ограничения на пропускную способность в задаче не определены, то есть по всем дорогам можем провозить любое количество груза.
Перейдем к основным соотношениям для потока. Первый узел является истоком, из него можем добраться в города 2, 3 и 4. Объем заказа составляет одну единицу, значит, производительность истока равна 1. Втекающий поток отсутствует, следовательно:
$\displaystyle x_{12} +x_{13} +x_{14} =1$ (узел 1)
Рассмотрим основное соотношение для промежуточных узлов сети. Известно, что их производительность равна нулю. Выехать из города 2 можно лишь в города 4 и 5, а попасть в город 2 можно только из города 1, значит, соотношение для узла 2 имеет вид:
$\displaystyle (x_{24} +x_{25} )-x_{12} =0$ (узел 2)
Рассуждая аналогично, для оставшихся четырех узлов получим:
$\displaystyle (x_{34} +x_{36} )-x_{13} =0$ (узел 3)
$\displaystyle (x_{45} +x_{46} +x_{47} )-(x_{14} +x_{24} +x_{34} )=0$ (узел 4)
$\displaystyle x_{57} -(x_{25} +x_{45} )=0$ (узел 5)
$\displaystyle x_{67} -(x_{46} +x_{36} )=0$ (узел 6)
В узел 7 можно попасть из узлов 4, 5 и 6. Вытекающий поток из узла 7 отсутствует. Считая спрос отрицательной производительностью, имеем ограничение для стока:
$\displaystyle -(x_{47} +x_{57} +x_{67} )=-1$ (узел 7).
Учтем неотрицательность и целочисленность потока:
$x_{ij} \ge 0$ , $x_{ij} $ - целые
{\it 3.2. Реализация задачи о кратчайшем пути в Excel}{\it }(см. файл 2КомфортКратчайший путь.xls)
Откроем лист "допустимое решение". Определим кратчайший путь, согласно схеме дорог из примера пункта 3.1.
Как и ранее, ячейки, содержащие параметры задачи, будем выделять серым цветом и обводить в синие рамки. Ячейки, содержащие переменные, будем обводить красными рамками.
{\bf Исходные данные}
В ячейках B8:M8 указываем расстояния между городами
В ячейках B9:M15 указываем коэффициенты, соответствующие вытекающему и втекающему потоку в каждый узел. Здесь достаточно указать лишь значения 1 и -1. Содержимое пустых ячеек интерпретируются как 0.
В ячейках P9:P15 указываем производительность узлов
В ячейках В6:М6 указываем произвольный допустимый путь между истоком и стоком, например, 1>2>5>7. Для этого необходимо присвоить значения 1 переменным $x_{12} $ , $x_{25} $ , $x_{57} $ . Остальным переменным присваиваем нулевые значения.
{\bf Ограничения}
В ячейке N9 указываем суммарный поток, вытекающий из узла 1:
=СУММПРОИЗВ(\$B\$6:\$M\$6;B9:M9).
Здесь используется абсолютная адресация на массив ячеек, содержащих переменные задачи: \$B\$6:\$M\$6 и относительная адресация на коэффициенты ограничений: B9:M9. Это позволяет корректно скопировать формулу в ячейки, соответствующие оставшимся узлам: N10:N15.
{\bf Целевая функция}
В ячейке А19 подсчитывается общая длина пути с помощью формулы:
=СУММПРОИЗВ(C6:E7;C12:E13).
Длина пути 1>2>5>7 равна 80.
{\bf Поиск решения}
Перейдем на лист "оптимальное решение", откроем надстройку "Поиск решения".
{\it Установить целевую ячейку.} Указываем ячейку А19 - длина пути
{\it Изменяемые ячейки.} Выбираем массив \$B\$6:\$M\$6 в качестве изменяемых ячеек.
{\it Ограничения.} Добавляем ограничения на значение вытекающего и втекающего потоков для каждого из семи узлов: \$N\$9:\$N\$15=\$P\$9:\$P\$15, а также целочисленность и неотрицательность переменных: \$B\$6:\$M\$6=целое, \$B\$6:\$M\$6?0.
Нажимаем кнопку Параметры и устанавливаем флаг в поле Линейная модель. Возвращаемся в диалоговое окно Поиска решения и нажимаем Выполнить.
В результате проведенной оптимизации единичные значения были присвоены следующим переменным: $x_{13} =1$ , $x_{36} =1$ , $x_{67} =1$ . Остальные переменные равны нулю. Это соответствует пути 1>3>6>7. Длина этого пути указана в целевой ячейке и равна 68.
Сетевая интерпретация решения:
Обратим внимание, что в задаче фирмы "Комфорт" необходимо было доставить клиенту один эксклюзивный стол. Разумеется, получившийся в результате решения оптимизационной задачи кратчайший путь, не зависит от объема заказа. Поэтому в общей постановке задачи о кратчайшем пути всегда предполагается, что производительность истока (стока) равна 1 (минус 1).




